What is a dozen? Well, a dozen is 12 of something. It is a natural counting number, because I can count to 12 using the thumb and finger joints of ONE hand. A Baker’s dozen is 13. Avogadro’s number is defined as the number of elementary particles (molecules, atoms, compounds, etc.) per mole of a substance. It is equal to 6.022×10 23 mol -1 and is expressed as the symbol N A. Avogadro’s number is a similar concept to that of a dozen or a gross. A dozen molecules is 12 molecules.
Aug 25, 2020 The mole is defined as the amount of substance that contains the number of carbon atoms in exactly 12 g of carbon-12, Avogadro’s number (6.022 × 10 23) of atoms of carbon-12. Avogadro’s number provides a startling glimpse into the tiny size of atoms. For example, one gram-mole of water has a mass of 18 grams, equivalent to about 0.63 ounces and containing 6.02214179 × 10 23 molecules. The same number of sand grains would be found in a 50-foot-deep layer of fine sand covering the entire state of Texas (the.
Contrary to the beliefs of generations of chemistry students, Avogadro’s number—the number of particles in a unit known as a mole—was not discovered by Amadeo Avogadro (1776-1856). Avogadro was a lawyer who became interested in mathematics and physics, and in 1820 he became the first professor of physics in Italy. Avogadro is most famous for his hypothesis that equal volumes of different gases at the same temperature and pressure contain the same number of particles.
The first person to estimate the actual number of particles in a given amount of a substance was Josef Loschmidt, an Austrian high school teacher who later became a professor at the University of Vienna. In 1865 Loschmidt used kinetic molecular theory to estimate the number of particles in one cubic centimeter of gas at standard conditions. This quantity is now known as the Loschmidt constant, and the accepted value of this constant is 2.6867773 x 1025 m-3.
The term “Avogadro’s number” was first used by French physicist Jean Baptiste Perrin. In 1909 Perrin reported an estimate of Avogadro’s number based on his work on Brownian motion—the random movement of microscopic particles suspended in a liquid or gas. In the years since then, a variety of techniques have been used to estimate the magnitude of this fundamental constant.
Accurate determinations of Avogadro’s number require the measurement of a single quantity on both the atomic and macroscopic scales using the same unit of measurement. This became possible for the first time when American physicist Robert Millikan measured the charge on an electron. The charge on a mole of electrons had been known for some time and is the constant called the Faraday. The best estimate of the value of a Faraday, according to the National Institute of Standards and Technology (NIST), is 96,485.3383 coulombs per mole of electrons. The best estimate of the charge on an electron based on modern experiments is 1.60217653 x 10-19 coulombs per electron. If you divide the charge on a mole of electrons by the charge on a single electron you obtain a value of Avogadro’s number of 6.02214154 x 1023 particles per mole.
Another approach to determining Avogadro’s number starts with careful measurements of the density of an ultrapure sample of a material on the macroscopic scale. The density of this material on the atomic scale is then measured by using x-ray diffraction techniques to determine the number of atoms per unit cell in the crystal and the distance between the equivalent points that define the unit cell (see Physical Review Letters, 1974, 33, 464).
Learning Objectives
By the end of this section, you will be able to:
- Define the amount unit mole and the related quantity Avogadro’s number
- Explain the relation between mass, moles, and numbers of atoms or molecules, and perform calculations deriving these quantities from one another
The Mole
The identity of a substance is defined not only by the types of atoms or ions it contains, but by the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, we possess sophisticated instruments that allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for amount of substances, the mole, which remains indispensable in modern chemical science.
The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter. A mole is defined as the amount of substance containing the same number of discrete entities (atoms, molecules, ions, etc.) as the number of atoms in a sample of pure 12C weighing exactly 12 g. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth.
The number of entities composing a mole has been experimentally determined to be [latex]6.02214179times {10}^{23}[/latex], a fundamental constant named Avogadro’s number(NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being [latex]6.022times {10}^{23}text{/mol}[/latex].
Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol) (see Figure 1).
Figure 1. Each sample contains 6.022 × 1023 atoms—1.00 mol of atoms. From left to right (top row): 65.4g zinc, 12.0g carbon, 24.3g magnesium, and 63.5g copper. From left to right (bottom row): 32.1g sulfur, 28.1g silicon, 207g lead, and 118.7g tin. (credit: modification of work by Mark Ott)
Because the definitions of both the mole and the atomic mass unit are based on the same reference substance, 12C, the molar mass of any substance is numerically equivalent to its atomic or formula weight in amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). According to the definition of the mole, 12 g of 12C contains 1 mole of 12C atoms (its molar mass is 12 g/mol). This relationship holds for all elements, since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu (Figure 2).
Figure 2. Each sample contains 6.02 × 1023 molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.9g of HgI2 (mercury(II) iodide, formula mass 459.9 amu), 32.0g of CH3OH (methanol, formula mass 32.0 amu) and 256.5g of S8 (sulfur, formula mass 256.6 amu). (credit: Sahar Atwa)
| Element | Average Atomic Mass (amu) | Molar Mass (g/mol) | Atoms/Mole |
|---|---|---|---|
| C | 12.01 | 12.01 | [latex]6.022times {10}^{23}[/latex] |
| H | 1.008 | 1.008 | [latex]6.022times {10}^{23}[/latex] |
| O | 16.00 | 16.00 | [latex]6.022times {10}^{23}[/latex] |
| Na | 22.99 | 22.99 | [latex]6.022times {10}^{23}[/latex] |
| Cl | 33.45 | 33.45 | [latex]6.022times {10}^{23}[/latex] |
While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g (see Figure 3). The number of molecules in a single droplet of water is roughly 100 billion times greater than the number of people on earth.
Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.
The mole is used in chemistry to represent [latex]6.022times {10}^{23}[/latex] of something, but it can be difficult to conceptualize such a large number. Watch this video to learn more.
The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.
Example 1: Deriving Moles from Grams for an Element
According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?
Show AnswerThe mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.
The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):
The factor-label method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:”
[latex]4.7cancel{text{g}}text{K}left(frac{text{mol K}}{39.10cancel{text{g}}}right)=0.12text{mol K}[/latex]
The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation, since it is a bit greater than 0.1 mol.
Check Your Learning
Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?
Example 2: Deriving Grams from Moles for an Element
A liter of air contains [latex]9.2times {10}^{-4}[/latex] mol argon. What is the mass of Ar in a liter of air?
Show AnswerThe molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10–3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

In this case, logic dictates (and the factor-label method supports) multiplying the provided amount (mol) by the molar mass (g/mol):
Mole And Avogadro's Number Explained
[latex]9.2times {10}^{-4}cancel{text{mol}}text{Ar}left(frac{39.95text{g}}{cancel{text{mol}}text{Ar}}right)=0.037text{g Ar}[/latex]
The result is in agreement with our expectations as noted above, around 0.04 g Ar.
Check Your Learning
What is the mass of 2.561 mol of gold?
Example 3: Deriving Number of Atoms from Mass for an Element
Copper is commonly used to fabricate electrical wire (Figure 7). How many copper atoms are in 5.00 g of copper wire?
Figure 7. Copper wire is composed of many, many atoms of Cu. (credit: Emilian Robert Vicol)
Show AnswerThe number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to number of Cu atoms:
Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:
[latex]5.00cancel{text{g}}text{Cu}left(frac{cancel{text{mol}}text{Cu}}{63.55cancel{text{g}}}right)left(frac{6.022times {10}^{23}text{atoms}}{cancel{text{mol}}}right)=4.74times {10}^{22}text{atoms of copper}[/latex]
The factor-label method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.
Check Your Learning
A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?
Show AnswerExample 4: Deriving Moles from Grams for a Compound
Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?
Show AnswerWe can derive the number of moles of a compound from its mass following the same procedure we used for an element in Example 3:
The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:
The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:
[latex]28.35cancel{text{g}}text{glycine}left(frac{text{mol glycine}}{75.07cancel{text{g}}}right)=0.378text{ mol glycine}[/latex]
This result is consistent with our rough estimate.
Check Your Learning
How many moles of sucrose, C12H22O11, are in a 25-g sample of sucrose?
Example 5: Deriving Grams from Moles for a Compound
Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is [latex]1.42times {10}^{-4}text{mol.}[/latex] What is the mass of this allowance in grams?
Show AnswerAs for elements, the mass of a compound can be derived from its molar amount as shown:
The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10-4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:
[latex]1.42times {10}^{-4}cancel{text{mol}}text{vitamin C}left(frac{176.124text{g}}{cancel{text{mol}}text{vitamin C}}right)=0.0250text{g vitamin C}[/latex]
This is consistent with the anticipated result.
Check Your Learning
What is the mass of 0.443 mol of hydrazine, N2H4?
Example 6: Deriving the Number of Atoms and Molecules from the Mass of a Compound
A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula:
Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?
Show AnswerThe number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated in Figure 5, and then multiplying by Avogadro’s number:
Using the provided mass and molar mass for saccharin yields:
[latex]0.0400cancel{text{g}}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S}left(frac{cancel{text{mol}}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S}}{183.18cancel{text{g}}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S}}right)left(frac{6.022times {10}^{23}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S molecules}}{1cancel{text{mol}}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S}}right)=1.31times {10}^{20}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S molecules}[/latex]
The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:
[latex]1.31times {10}^{20}{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S molecules}left(frac{7text{C atoms}}{1{text{C}}_{7}{text{H}}_{5}{text{NO}}_{3}text{S molecule}}right)=9.20times {10}^{21}text{C atoms}[/latex]
Check Your Learning
How many C4H10 molecules are contained in 9.213 g of this compound? How many hydrogen atoms?
Show Answer[latex]9.545times {10}^{22}text{molecules }{text{C}}_{4}{text{H}}_{10}text{; }9.545times {10}^{23}text{ atoms H}[/latex]
Key Concepts and Summary
A convenient amount unit for expressing very large numbers of atoms or molecules is the mole. Experimental measurements have determined the number of entities composing 1 mole of substance to be [latex]6.022times {10}^{23}[/latex], a quantity called Avogadro’s number. The mass in grams of 1 mole of substance is its molar mass. Due to the use of the same reference substance in defining the atomic mass unit and the mole, the formula mass (amu) and molar mass (g/mol) for any substance are numerically equivalent (for example, one H2O molecule weighs approximately18 amu and 1 mole of H2O molecules weighs approximately 18 g).

Exercises
- Write a sentence that describes how to determine the number of moles of a compound in a known mass of the compound if we know its molecular formula.
- Compare 1 mole of H2, 1 mole of O2, and 1 mole of F2.
- Which has the largest number of molecules? Explain why.
- Which has the greatest mass? Explain why.
- Which contains the greatest mass of oxygen: 0.75 mol of ethanol (C2H5OH), 0.60 mol of formic acid (HCO2H), or 1.0 mol of water (H2O)? Explain why.
- Which contains the greatest number of moles of oxygen atoms: 1 mol of ethanol (C2H5OH), 1 mol of formic acid (HCO2H), or 1 mol of water (H2O)? Explain why.
- How are the molecular mass and the molar mass of a compound similar and how are they different?
- Calculate the molar mass of each of the following compounds:
- hydrogen fluoride, HF
- ammonia, NH3
- nitric acid, HNO3
- silver sulfate, Ag2SO4
- boric acid, B(OH)3
- Calculate the molar mass of each of the following:
- S8
- C5H12
- Sc2(SO4)3
- CH3COCH3 (acetone)
- C6H12O6 (glucose)
- Calculate the molar mass of each of the following minerals:
- limestone, CaCO3
- halite, NaCl
- beryl, Be3Al2Si6O18
- malachite, Cu2(OH)2CO3
- turquoise, CuAl6(PO4)4(OH)8(H2O)4
- Calculate the molar mass of each of the following:
- the anesthetic halothane, C2HBrClF3
- the herbicide paraquat, C12H14N2Cl2
- caffeine, C8H10N4O2
- urea, CO(NH2)2
- a typical soap, C17H35CO2Na
- Determine the number of moles of compound and the number of moles of each type of atom in each of the following:
- 25.0 g of propylene, C3H6
- [latex]3.06times {10}^{-3}text{g}[/latex] of the amino acid glycine, C2H5NO2
- 25 lb of the herbicide Treflan, C13H16N2O4F (1 lb = 454 g)
- 0.125 kg of the insecticide Paris Green, Cu4(AsO3)2(CH3CO2)2
- 325 mg of aspirin, C6H4(CO2H)(CO2CH3)
- Determine the mass of each of the following:
- 0.0146 mol KOH
- 10.2 mol ethane, C2H6
- [latex]1.6times {10}^{-3}text{ mol }{text{Na}}_{2}{text{SO}}_{4}[/latex]
- [latex]6.854times {10}^{3}text{ mol glucose},{text{C}}_{6}{text{H}}_{12}{text{O}}_{6}[/latex]
- 2.86 mol Co(NH3)6Cl3
- Determine the number of moles of the compound and determine the number of moles of each type of atom in each of the following:
- 2.12 g of potassium bromide, KBr
- 0.1488 g of phosphoric acid, H3PO4
- 23 kg of calcium carbonate, CaCO3
- 78.452 g of aluminum sulfate, Al2(SO4)3
- 0.1250 mg of caffeine, C8H10N4O2
- Determine the mass of each of the following:
- 2.345 mol LiCl
- 0.0872 mol acetylene, C2H2
- [latex]3.3times {10}^{-2}text{ mol }{text{Na}}_{2}{text{CO}}_{3}[/latex]
- [latex]1.23times {10}^{3}text{ mol fructose, }{text{C}}_{6}{text{H}}_{12}{text{O}}_{6}[/latex]
- 0.5758 mol FeSO4(H2O)7
- The approximate minimum daily dietary requirement of the amino acid leucine, C6H13NO2, is 1.1 g. What is this requirement in moles?
- Determine the mass in grams of each of the following:
- 0.600 mol of oxygen atoms
- 0.600 mol of oxygen molecules, O2
- 0.600 mol of ozone molecules, O3
- A 55-kg woman has [latex]7.5times {10}^{-3}text{mol}[/latex] of hemoglobin (molar mass = 64,456 g/mol) in her blood. How many hemoglobin molecules is this? What is this quantity in grams?
- Determine the number of atoms and the mass of zirconium, silicon, and oxygen found in 0.3384 mol of zircon, ZrSiO4, a semiprecious stone.
- Determine which of the following contains the greatest mass of hydrogen: 1 mol of CH4, 0.6 mol of C6H6, or 0.4 mol of C3H8.
- Determine which of the following contains the greatest mass of aluminum: 122 g of AlPO4, 266 g of Al2Cl6, or 225 g of Al2S3.
- Diamond is one form of elemental carbon. An engagement ring contains a diamond weighing 1.25 carats (1 carat = 200 mg). How many atoms are present in the diamond?
- The Cullinan diamond was the largest natural diamond ever found (January 25, 1905). It weighed 3104 carats (1 carat = 200 mg). How many carbon atoms were present in the stone
- One 55-gram serving of a particular cereal supplies 270 mg of sodium, 11% of the recommended daily allowance. How many moles and atoms of sodium are in the recommended daily allowance?
- A certain nut crunch cereal contains 11.0 grams of sugar (sucrose, C12H22O11) per serving size of 60.0 grams. How many servings of this cereal must be eaten to consume 0.0278 moles of sugar?
- A tube of toothpaste contains 0.76 g of sodium monofluorophosphate (Na2PO3F) in 100 mL
- What mass of fluorine atoms in mg was present?
- How many fluorine atoms were present?
- Which of the following represents the least number of molecules?
- 20.0 g of H2O (18.02 g/mol)
- 77.0 g of CH4 (16.06 g/mol)
- 68.0 g of CaH2 (42.09 g/mol)
- 100.0 g of N2O (44.02 g/mol)
- 84.0 g of HF (20.01 g/mol)
1. Use the molecular formula to find the molar mass; to obtain the number of moles, divide the mass of compound by the molar mass of the compound expressed in grams.
3. Formic acid. Its formula has twice as many oxygen atoms as the other two compounds (one each). Therefore, 0.60 mol of formic acid would be equivalent to 1.20 mol of a compound containing a single oxygen atom.
5.The two masses have the same numerical value, but the units are different: The molecular mass is the mass of 1 molecule while the molar mass is the mass of [latex]6.022times {10}^{23}[/latex] molecules.
7. The molecular mass of each compound is as follows:
- S8:
[latex]8text{S}=8times 32.066=256.528text{g/mol}[/latex] - C5H12:
[latex]begin{array}{lll}hfill 5text{C}=5times 12.011& =& 60.055text{g}{text{mol}}^{-1}hfill hfill text{12H}=12times 1.00794& =& underline{12.09528text{g}{text{mol}}^{-1}}hfill hfill & =& 72.150text{g}{text{mol}}^{-1}hfill end{array}[/latex] - Sc2(SO4)3:
[latex]begin{array}{lll}hfill 2text{Sc}=2times 44.9559109& =& 89.9118218text{g}{text{mol}}^{-1}hfill hfill text{3S}=3times 32.066& =& 96.198text{g}{text{mol}}^{-1}hfill hfill 12text{O}=12times 15.99943& =& underline{191.99316text{g}{text{mol}}^{-1}}hfill hfill & =& 378.103text{g}{text{mol}}^{-1}hfill end{array}[/latex] - CH3COCH3:
[latex]begin{array}{lll}hfill 3text{C}=3times 12.011& =& 36.033text{g}{text{mol}}^{-1}hfill hfill text{1O}=1times 15.9994& =& 15.9994text{g}{text{mol}}^{-1}hfill hfill 6text{H}=6times 1.00794& =& underline{6.04764text{g}{text{mol}}^{-1}}hfill hfill & =& 58.080text{g}{text{mol}}^{-1}hfill end{array}[/latex] - C6H12O6:
[latex]begin{array}{lll}hfill text{6C}=6times 12.011& =& 72.066text{g}{text{mol}}^{-1}hfill hfill text{12H}=12times 1.00794& =& 12.09528text{g}{text{mol}}^{-1}hfill hfill 6text{O}=6times 15.9994& =& underline{95.9964text{g}{text{mol}}^{-1}}hfill hfill & =& 180.158text{g}{text{mol}}^{-1}hfill end{array}[/latex]
9. The molecular mass of each compound is as follows:
- C2HBrClF3:
[latex]begin{array}{lll}hfill text{2C}=2times 12.011& =& 24.022text{g}{text{mol}}^{-1}hfill hfill text{1H}=1times 1.00794& =& 1.00794text{g}{text{mol}}^{-1}hfill hfill text{1Br}=1times 79.904& =& 79.904text{g}{text{mol}}^{-1}hfill hfill text{1Cl}=1times 35.453& =& 35.453text{g}{text{mol}}^{-1}hfill hfill 3text{F}=3times 18.998403& =& underline{56.995209text{g}{text{mol}}^{-1}}hfill hfill & =& 197.682text{g}{text{mol}}^{-1}hfill end{array}[/latex] - C12H14N2Cl2:
[latex]begin{array}{lll}hfill text{12C}=12times 12.011& =& 144.132text{g}{text{mol}}^{-1}hfill hfill text{14H}=14times 1.00794& =& 14.111text{g}{text{mol}}^{-1}hfill hfill text{2N}=2times 14.0067& =& 28.0134text{g}{text{mol}}^{-1}hfill hfill text{2Cl}=2times 35.453& =& underline{70.906text{g}{text{mol}}^{-1}}hfill hfill & =& 257.163text{g}{text{mol}}^{-1}hfill end{array}[/latex] - C8H10N4O2:
[latex]begin{array}{lll}hfill text{8C}=8times 12.011& =& 96.088text{g}{text{mol}}^{-1}hfill hfill text{10H}=10times 1.007& =& 10.079text{g}{text{mol}}^{-1}hfill hfill text{4N}=4times 14.0067& =& 56.027text{g}{text{mol}}^{-1}hfill hfill text{2O}=2times 15.9994& =& underline{31.999text{g}{text{mol}}^{-1}}hfill hfill & =& 194.193text{g}{text{mol}}^{-1}hfill end{array}[/latex] - CO(NH2)2:
[latex]begin{array}{lll}hfill text{1C}=1times 12.011& =& 12.011text{g}{text{mol}}^{-1}hfill hfill text{1O}=1times 15.9994& =& 15.9994text{g}{text{mol}}^{-1}hfill hfill text{2N}=2times 14.0067& =& 28.0134text{g}{text{mol}}^{-1}hfill hfill text{4H}=4times 1.00794& =& underline{4.03176text{g}{text{mol}}^{-1}}hfill hfill & =& 60.056text{g}{text{mol}}^{-1}hfill end{array}[/latex] - C17H35CO2Na:
[latex]begin{array}{lll}hfill text{18C}=18times 12.011& =& 216.198text{g}{text{mol}}^{-1}hfill hfill text{35H}=35times 1.00794& =& 35.2779text{g}{text{mol}}^{-1}hfill hfill text{2O}=2times 15.9994& =& 31.9988text{g}{text{mol}}^{-1}hfill hfill text{1Na}=1times 22.98977& =& underline{22.98977text{g}{text{mol}}^{-1}}hfill hfill & =& 306.464text{g}{text{mol}}^{-1}hfill end{array}[/latex]
11. The mass of each compound is as follows:
- KOH:
[latex]begin{array}{lll}hfill 1text{K}=1times 39.0983& =& 39.0983hfill hfill 1text{O}=1times 15.9994& =& 15.9994hfill hfill text{1H}=1times 1.00794& =& underline{1.00794}hfill hfill text{molar mass}& =& 56.1056text{g}{text{mol}}^{-1}hfill end{array}[/latex]
[latex]text{Mass}=0.0146text{mol}times 56.1056text{g/mol}=0.819text{g}[/latex] - C2H6:
[latex]begin{array}{lll}hfill 2text{C}=2times 12.011& =& 24.022hfill hfill 6text{H}=6times 1.00794& =& underline{6.04764}hfill hfill text{molar mass}& =& 30.070text{g}{text{mol}}^{-1}hfill end{array}[/latex]
[latex]text{Mass}=10.2text{mol}times 30.070text{g/mol}=307text{g}[/latex] - Na2SO4:
[latex]begin{array}{lll}hfill 2text{Na}=2times 22.990& =& 45.98hfill hfill 1text{S}=1times 32.066& =& 32.066hfill hfill 4text{O}=4times 15.9994& =& underline{63.9976}hfill hfill text{molar mass}& =& 142.044text{g}{text{mol}}^{-1}hfill end{array}[/latex]
[latex]text{Mass}=1.6times {10}^{-3}text{mol}times 142.044text{g/mol}=text{0.23 g}[/latex] - C6H12O6:
[latex]begin{array}{lll}hfill 6text{C}=6times 12.011& =& 72.066hfill hfill 12text{H}=12times 1.00794& =& 12.0953hfill hfill 6text{O}=6times 15.9994& =& underline{95.9964}hfill hfill text{molar mass}& =& 180.158text{g}{text{mol}}^{-1}hfill end{array}[/latex]
[latex]text{Mass}=6.854times {10}^{3}text{mol}times 180.158text{g/mol}=1.235times {10}^{6}text{g (}1235text{kg)}[/latex] - Co(NH3)6Cl3:
[latex]begin{array}{lll}hfill text{Co}=1times 58.99320& =& 58.99320hfill hfill 6text{N}=6times 14.0067& =& 84.0402hfill hfill 18text{H}=18times 1.00794& =& 18.1429hfill hfill 3text{Cl}=3times 35.4527& =& underline{106.358}hfill hfill text{molar mass}& =& 267.5344text{g}{text{mol}}^{-1}hfill end{array}[/latex]
[latex]text{Mass}=2.856text{mol}times 267.5344text{g/mol}=765text{g}[/latex]
13.
- 2.345 mol LiCl:
[latex]begin{array}{lll}hfill text{molar mass}left(text{LiCl}right)=1times 6.941+1times 35.4527& =& 42.394text{g}{text{mol}}^{-1}hfill hfill text{mass}=2.345cancel{text{mol}}times 42.394text{g}cancel{{text{mol}}^{-1}}& =& 99.41text{g}hfill end{array}[/latex] - 0.0872 mol acetylene, C2H2:
[latex]begin{array}{lll}hfill text{molar mass}left({text{C}}_{2}{text{H}}_{2}right)=2times 12.011+2times 1.00794& =& 26.038text{g}{text{mol}}^{-1}hfill hfill text{mass}=0.0872cancel{text{mol}}times 26.038text{g}cancel{{text{mol}}^{-1}}& =& 2.27text{g}hfill end{array}[/latex] - 3.3 × 10−2 mol Na2CO3:
[latex]begin{array}{lll}hfill text{molar mass}left({text{Na}}_{2}{text{CO}}_{3}right)=2times 22.989768+1times 12.011+3times 15.9994& =& 105.989text{g}{text{mol}}^{-1}hfill hfill text{mass}=3.3times {10}^{-2}cancel{text{mol}}times 105.989text{g}{text{mol}}^{-1}& =& 3.5text{g}hfill end{array}[/latex] - 1.23 × 103 mol fructose, C6H12O6:[latex]begin{array}{lll}hfill text{molar mass}left({text{C}}_{6}{text{H}}_{12}{text{O}}_{6}right)=6times 12.011+12times 1.00794+6times 15.9994& =& 180.158text{g}{text{mol}}^{-1}hfill hfill text{mass}=1.23times {10}^{3}cancel{text{mol}}times 180.158text{g}{text{mol}}^{-1}=2.22times {10}^{5}text{g}& =& 222text{kg}hfill end{array}[/latex]
- 0.5758 mol FeSO4(H2O)7:
[latex]begin{array}{lll}hfill text{molar mass}left[{text{FeSO}}_{4}{left({text{H}}_{2}text{O}right)}_{7}right]& =& 1times 55.847+1times 32.066+4times 15.999hfill hfill +7left(2times 1.00794+15.9994right)& =& 278.018text{g}{text{mol}}^{-1}hfill hfill text{mass}=0.5758cancel{text{mol}}times 278.018text{g}cancel{{text{mol}}^{-1}}& =hfill & 160.1text{g}hfill end{array}[/latex]
15. The mass of each compound is as follows:
- [latex]0.600cancel{text{mol}}times 15.9994text{g/}cancel{text{mol}}=9.60text{g}[/latex]
- [latex]0.600cancel{text{mol}}times 2times 15.994text{g/}cancel{text{mol}}=19.2text{g}[/latex]
- [latex]0.600cancel{text{mol}}times 3times 15.994text{g/}cancel{text{mol}}=28.8text{g}[/latex]
17. Determine the number of moles of each component. From the moles, calculate the number of atoms and the mass of the elements involved. Zirconium: [latex]0.3384cancel{text{mol}}times 6.022times {10}^{23}{cancel{text{mol}}}^{cancel{-1}}=2.038times 1023text{atoms;}0.3384cancel{text{mol}}times 91.224text{g/}cancel{text{mol}}=30.87text{g;}[/latex] Silicon: [latex]0.3384cancel{text{mol}}times 6.022times {10}^{23}{cancel{text{mol}}}^{cancel{-1}}=2.038times {10}^{23}text{atoms;}0.3384cancel{text{mol}}times 28.0855text{g/}cancel{text{mol}}=9.504text{g;}[/latex] Oxygen: [latex]4times 0.3384cancel{text{mol}}times 6.022times {10}^{23}{cancel{text{mol}}}^{cancel{-1}}=8.151times {10}^{23}text{atoms;}4times 0.3384cancel{text{mol}}times 15.9994text{g/}cancel{text{mol}}=21.66text{g}[/latex]
19. Determine the molar mass and, from the grams present, the moles of each substance. The compound with the greatest number of moles of Al has the greatest mass of Al.
- Molar mass AlPO4: 26.981539 + 30.973762 + 4(15.9994) = 121.9529 g/mol
- Molar mass Al2Cl6: 2(26.981539) + 6(35.4527) = 266.6793 g/mol
- Molar mass Al2S3: 2(26.981539) + 3(32.066) = 150.161 g/mol
AlPO4: [latex]frac{122cancel{text{g}}}{121.9529cancel{text{g}}{text{mol}}^{-1}}=1.000text{mol.}[/latex]
[latex]text{mol Al}=1times 1.000text{mol}=1.000text{mol}[/latex]
Al2Cl6: [latex]frac{266text{g}}{266.6793text{g}{text{mol}}^{-1}}=0.997text{mol}[/latex]
[latex]text{mol Al}=2times 0.997text{mol}=1.994text{mol}[/latex]
Al2S3: [latex]frac{225cancel{text{g}}}{150.161cancel{text{g}}{text{mol}}^{-1}}=1.50text{mol}[/latex]
The Avogadro Number

[latex]text{mol Al}=2times 1.50text{mol}=3.00text{mol}[/latex]
21. Determine the number of grams present in the diamond and from that the number of moles. Find the number of carbon atoms by multiplying Avogadro’s number by the number of moles:
[latex]frac{3104cancel{text{carats}}times frac{200cancel{text{mg}}}{1cancel{text{carat}}}times frac{1cancel{text{g}}}{1000cancel{text{mg}}}}{12.011cancel{text{g}}cancel{{text{mol}}^{-1}}left(6.022times {10}^{23}cancel{{text{mol}}^{-1}}right)}=3.113times {10}^{25}text{C atoms}[/latex]
23. Determine the molar mass of sugar. 12(12.011) + 22(1.00794) + 11(15.9994) = 342.300 g/mol; Then [latex]0.0278text{mol}times 342.300text{g/mol}=9.52text{g sugar.}[/latex] This 9.52 g of sugar represents [latex]frac{11.0}{60.0}[/latex] of one serving or
Mole Avogadro's Number Worksheet

[latex]frac{60.0text{g serving}}{11.0cancel{text{g sugar}}}times 9.52cancel{text{g sugar}}=51.9text{g cereal.}[/latex]
This amount is [latex]frac{51.9text{g cereal}}{60.0text{g serving}}=0.865[/latex] servings, or about 1 serving.
25. Calculate the number of moles of each species, then remember that 1 mole of anything [latex]=6.022times {10}^{23}[/latex] species.
- 20.0 g = 1.11 mol H2O
- 77.0 g CH4 = 4.79 mol CH4
- 68.0 g CaH2 = 1.62 mol CaH2
- 100.0 g N2O = 2.27 mol N2O
- 84.0 g HF = 4.20 mol HF
Therefore, 20.0 g H2O represents the least number of molecules since it has the least number of moles.
Glossary
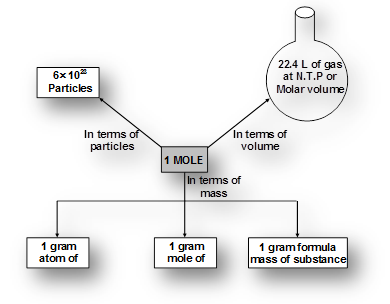
Avogadro's Number And Mole Concept Chart
Avogadro’s number (NA): experimentally determined value of the number of entities comprising 1 mole of substance, equal to [latex]6.022times {10}^{23}{text{mol}}^{-1}[/latex]
Avogadro's Number And Mole Concept Diagram
molar mass: mass in grams of 1 mole of a substance
mole: amount of substance containing the same number of atoms, molecules, ions, or other entities as the number of atoms in exactly 12 grams of 12C
